徐 进

(盐城工学院 ,江苏 盐城  224300)

摘 要: 丝杆升降机构传动在机械行业有广泛的应用,要求它在规定 时间内可靠地支撑起另外机构。就丝杆机构的运动特点,建立了机构失效模式及可靠性分析,创建了动力学方程,对传动的可靠性作了深入的研究,给出了传动动作和时间可靠度的求解方法,对提高本机构的可靠性具有重大意义。

关键词: 丝杆机构 传动 可靠性 设计

中图号: TH211      文献标识码：A

1 前言

丝杆升降传动机构在矿山机械行业中有广泛的应用 ,但对其传动进行可靠性研究未见文章报道。丝杆机构的结构简图如图1所示,由电机经安全离合器、圆锥齿轮及行星齿轮减速器带动丝杠旋转,螺母移动,顶起机件。为保证机构能够可靠地工作,除必须保证承载构件有足够的强度和刚度外,还必须保证机构的动作可靠性。即机构在规定的条件和时间内完成其规定动作的概率。

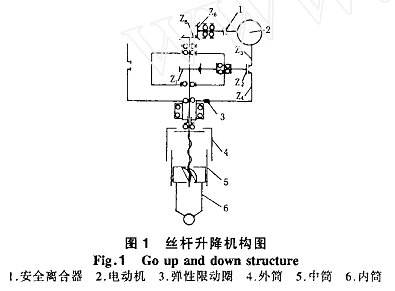
2 机构的失效模式及可靠性分析

经过分析,机构的主要失效形式有起动失效、继续运转失效、制动停车失效、定位失效、卡住失效和强度失效。

机构在不发生上述故障的前提下,要实现预定的动作 ,一般需经历如下几个阶段:保持初始静止状态 (锁紧初状态);开锁;起动;继续动转;制动、停车;定位、锁紧。

若上述6个阶段都能顺利地完成其动作,则认为机构动作可靠。若这6个阶段分别用事件E1、E2、E3、E4、E5、E6表示,对应可靠度用R1、R2、R3、R4、R5、R6表示。则机构的可靠度为

R=P{E1∩E2∩E3∩E4∩E5∩E6}   (1)

若上述事件相互独立 ,则

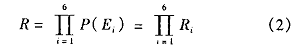
丝杆机构在工作前需进行初始状态的锁紧 ,一旦进人工作后 ,立 即解锁启动,顶起机构到预定位置,然后停车、定位、锁紧。其中E1、E2、E5、E6事件可以单独考虑 ,本文重点讨论起动和继续运转阶段的可靠性。

3  传动机构动作可靠性设计原理

根据文献 〔2〕,对于一个复杂的单自由度机械系统 ,可以将其简化为具有等效转动惯量或等效质量me 及其等效力矩Me(ψ,ω,t)(或 等效力Fe)的理想构件。力学模型如图 2所示。当等效构件的转角θ=0时 ,系统处于静止状态 （即前述 的第1阶段 ）。

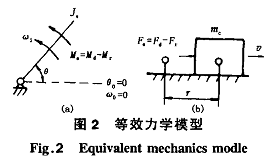
3.1  起动阶段的可靠性

要使机构达到一定的运转速度,原动机必须提供足够的驱动力矩Md ,克服该状态下的阻力矩Mt和惯性力矩,同时,也要以一定的加速度规律起动机构,保证其在较短的时间t内把转速从0提高到一定值ωm ,也就是说,在起动过程中,驱动力矩Md与阻力矩Mt的差值△ M要符合给定的规律,即

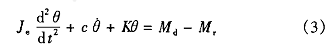
或

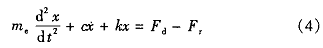
式 中

c —系统中的等效阻尼系数

k —系统中弹性构件的等效刚度系数

Md、Mr、Fd、Fr、—系统中的等效驱动力矩、等效阻力矩、等效驱动力、等效阻力。

求解上述微分方程 ,得到机构的运转速度θ达到ωm 时 ,所需 的时间(t1,   )

由于电机的驱动力矩Md是电流、电压、电阻、磁通、转矩常数等随机变量的函数。根据大数定理 ,将Md（或Fd）按正态分布处理,取其均值为Md（或Fd）均方差为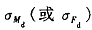，其大小可以通过测试确定。同理,阻力矩Mr ,也按正态分布处理 ,其均值和均方差分别面和  

机构在起动阶段克服阻力矩和惯性力矩的可靠度

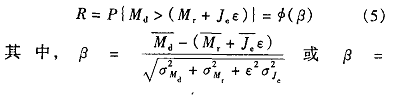
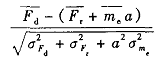
其 中 ,ε，α分别是系统允许的最低起动角加速度和加速度 。为 了计算方便,将其看成一个常数。如果系统对起动速度的快慢没有要求,可以将上式中与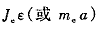有关的项去掉 。

根据式 （5）中的 β值查标准正态分布表 ,可求出R 值 。

3.2  继续运转阶段的可靠性

    机构在起动后，进入相对比较稳定的运转阶段，此时，原动机提供的驱动力矩Md接近或等于阻力矩Mr，故速度的波动较小。

    当Md>Mr时，机构的动能增加，即机构的运转速度增大。当Md0，机构就能够依靠惯性继续运动下去。

    故机构的可靠度

    R= P{Md -Mr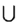≥0△W>0}

    但上述运算并不方便，可改用功的形式，以Ad和Ar分别表示Md和Mr所积累的功，则上式可改写成

R=P{Ad -Ar≥0}    (6)

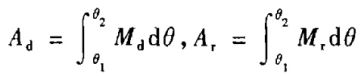
    上述Ad、Ar互为独立，服从于正态分布，故可靠性指标及可靠度

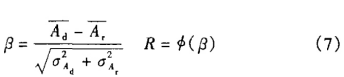
    若在连续运转阶段阻力矩逐渐加大，而且呈某种关系继续加大，初期能依靠惯性使机构继续运转，随后靠增大电机的输入电流来增大驱动力矩，克服阻力矩。此时，应单独划分为一个阶段，建立如式(3)、式、(4)的运动微分方程。求解后再用式(6)计算机构在此阶段的可靠度。

3.3在规定时间内完成动作的可靠度

    分阶段求出开锁、起动、继续运转、制动停车、定位锁紧5个阶段的时间分布状况。根据中心极限定理，总时间T也服从正态分布，即

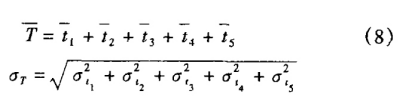
    在规定的时间T0内，完成动作的时间可靠度

4丝杆机构动作过程的可靠度计算

    将丝杆机构简化为图2(a)所示的等效构件，其回转中心为齿轮6和行星轮系的公共回转轴线，假定某瞬时电机轴的转速为ω1 (ω1 =ωm)，由于z5= z6，则等效构件的转动惯量

式中  J。——齿轮5、齿轮6、齿轮1、安全离合器、电机转子及转轴的转动惯量和；

      J2、m2——行星轮的转动惯量和质量；

v2——行星轮轴线的线速度；

 J4+ J4’——内齿轮和花键轴及弹性限动圈的转动惯量；

         ω4——角速度；

    Jgθ、ωgθ——丝杠的转动惯量及角速度；

      Mn、vn——螺母及套简的质量和移动速度。

4.1  丝杆机构的起动阶段

    如前所述，要保证丝杆机构可靠地起动，必须使系统的等效驱动力矩Md大于等效阻力矩Mr，此时，系统的阻力矩主要来自丝杠螺母的摩擦力矩，即

式中  Q——丝杠承受的轴向载荷，起动阶段为螺母及套筒的重量；

      d2——丝杠的螺纹中径；

       a——丝杠的螺旋升角；

      Ψ——丝杠螺旋的摩擦角。

    机构中的弹性限动圈为一弹性元件，扭转刚度为K。

    根据式(4)，运动微分方程为

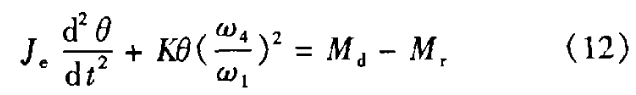
    由于齿轮啮合和轴承运转的阻力很小，可忽略不计，只计算螺纹的摩擦阻力矩Mgθ，故

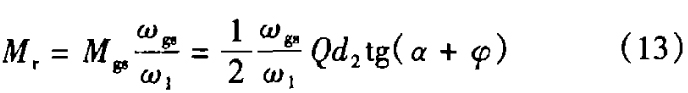
    求解式(12)，代人初始条件t=0、θ=0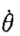， =0得

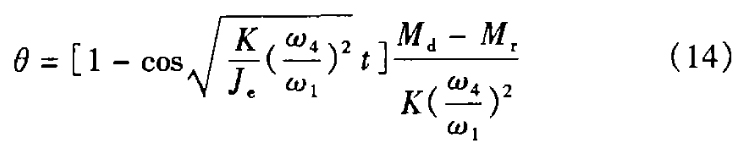
将式(14)对时间t求一阶、二阶导数，便可得到系统的速度和加速度。当系统进入稳定运转后，有θ=0，由此可求出加速过程的时间

与此对应的转角及速度为

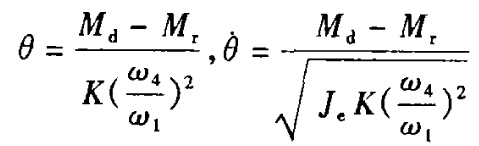
起动阶段的可靠度R3可按式(5)计算。

    丝杆机构的丝杠导程为P，起动阶段运行的距离

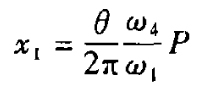
    由式(15)可求出起动阶段所需时间均值 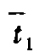。及均方差  。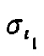

4.2丝杆机构的继续运转阶段

    丝杆机构在接触地面之前，负载较小，机构处于稳定运转状态。输出功都用来维持机构的运转，此阶段的可靠度可按式(6)计算。此时电机约转速为ωm，其运行时间的均值和方差为

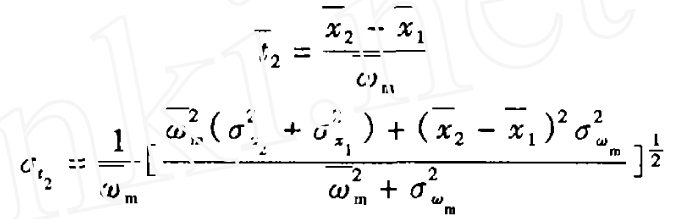
式中   ——丝杆机构接触地面时运行距离的均值和均方差。

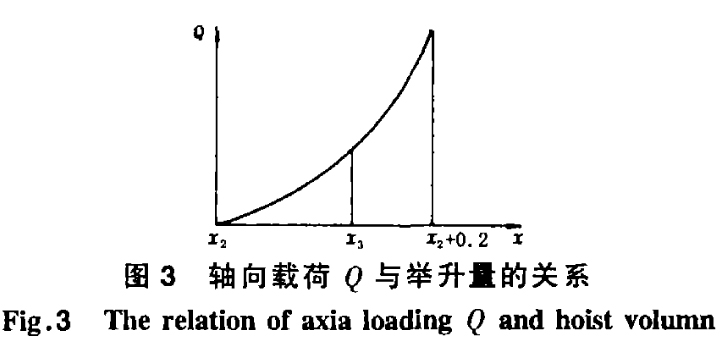
    丝杆机构接触地面后，载荷逐渐增大，千斤顶举升高度在规定值内，承受的轴向载荷Q与举升机件的高度（x - x 2）如图3所示，表达式为

Q =2 265(x - x 2)2+ 351.5（x - x 2）    (16)

    如图2(b)所示，将机构向丝杠螺母处简化，则机构的等效质量

建立机构运动微分方程，得

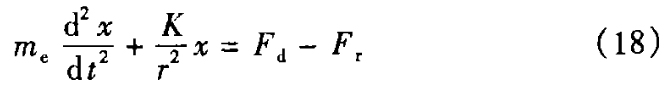
式中  r ——弹性限动圈的半径。

    考虑摩擦的影响，取F r = 1.1Q。丝杆机构驱动电机的输出转矩Md与其瞬时转速ω1有如下关系

Md=a+ bω1   (19)

式中  a、b ——电机的机械特性系数。

又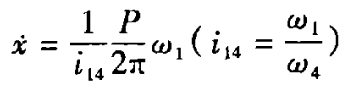    

得

    丝杠的回转力矩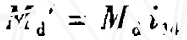，螺母上的等效驱动力

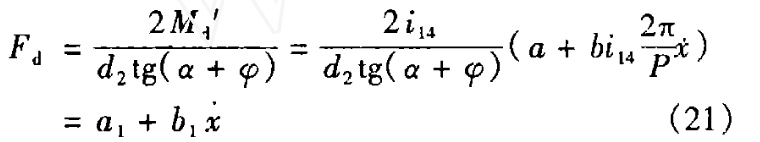
    将式(21)及式(16)代入式(18)，求解微分方程，再代入初始条件：t0=0，x0=x2，可求出。当机件被顶升到预定高度x3时，所需平均时间t3及均方差 。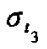

    此时，继续运转阶段的可靠度

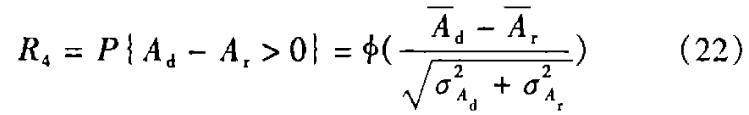
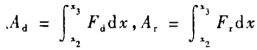式中     

4.3其余各阶段

    由于工作状态下机体可能很重，对丝杆机构产生的阻力矩很大，切断动力源后，丝杆机构能立即停车，故取此阶段的可靠度R5=1。

    丝杆机构的初始静止状态、开锁、定位锁紧阶段均有可靠的机械装置，其可靠度近似取为R1= R2=R6 =1。

    上述几个阶段所用时间很短，暂可忽略不计。

5结语

    最后，利用式(2)计算出系统的动作可靠度0.9852，利用式(8)和式(9)计算出在规定时间内完成动作的时间可靠度为0.9943。该数据表明这种方法可用于丝杆机构动作可靠性的分析计算，也可用于设计阶段技术指标中动作可靠性的评估，对提高机构及整个机器系统的可靠性具有重要意义。

参考文献：

[l]李良巧，机械可靠性设计与分析[M]．北京：国防工业出版社， 1998

[2]孙恒，机械原理[M]．北京：高等教育出版社，1993．

[3]周明溥，机构精度的概率设计[J]．机械设计，1986，(6)：27 - 28．

[4] Sandler B Z.Probahilistic approach to mechanisms[J].Elsevier, 1984.

    作者简介：徐进（1963 -）．硕士研究生，副教授，高级工程师，主要从事机械设计与制造教学科研工作，

收稿日期：2003-07-11

A study on the transmission reliability for silk pole hoist or                                                                                 lower or qanization

XU Jin

( Yancheng Institue of Technology , Yancheng 224003 , China)

Abstract: Silk pole hoist or lower organization transmission have extensive application mong mechananical homework , to require it reliable to support other organization within stilulatecl time , this text on silk pole sport characteristic of organization , set up orqanization invalid mode and dependability analyse , establish dynamic equation dependability in transmission make deep research give and offer transmission movement and ask method of solving time reliability, to improve dependability of mechanism have great meanings .

Key words: silk pole hoist or lower organization; transmission; reliability; design